Negative Feedback and Stability in Amplifiers

In this section I assume you already know the basic principles of negative feedback and how it is used in operational amplifiers (OpAmps) and amplifiers in general. Audio amplifiers, especially power amplifiers, employ the principle of global negative feedback, where portion of the output is fed back into the input stage of the amplifier and compared with the input signal, in order to increase linearity and frequency response of the amplifier. This principle is commonly used in OpAmps, where the user utilizes negative feedback (It is not employed inside the chip), and it is the same with discrete audio power amplifiers.

In Fig. 1 a generic opamp is depicted with a feedback network (β), which feeds back β portion of the output.

Fig.1 Generic amplifier with NFB

The loop gain is: 
$$ A_{loop}=A_{o} \cdot \beta $$

where Ao is the open loop gain of the amplifier and β is the portion of the output fed back to the input.

The output voltage is then:

$$ V_{out}=V_{in}\cdot \frac{A_{o}}{1+A_{o}\cdot \beta } $$

The feedback network and the amplifier itself consists of several components, which can introduce a delay in the signal, a phase-shift. (Remember that a simple RC low-pass filter for example introduces a 90 degree phase shift in the output voltage for frequencies above the cutoff (-3dB) frequency.)

If there is enough such delay to produce a 180 degree phase shift and the loop gain of the amplifier is greater or equal to unity (Av >= 1), then there will be positive feedback and the fed back signal will add to the input, resulting in oscillation of the amplifier.

(In modern electronics there is a term which is called phase margin: the difference of the actual phase shift and 180 degrees. In the presence of negative feedback a phase margin of 0 degrees at a frequency where loop gain is equal or greater to 1 leads to instability.
The lower safety limit for phase margin is 45 degrees. For example if at a signal frequency f the loop gain  is 1 and phase margin is below 45 degrees, it will lead to amplifier instability.)

The open loop bode plot of an opamp is depicted in Plot 1, where there is a pole frequency p1
after which gain decreases with 20db/decade rate. The vast majory of opamps in the market have a plot like this.

Plot 1. Open loop bode plot

The bode plot of an ideal negative feedback network is shown in Plot 2, where there are no poles and no phase shift.

Plot 2. Negative feedback bode plot

Combining the open loop and the negative feedback plots we get the loop gain bode plot of the amplifier as shown in Plot 3.

Plot 3. Loop gain bode plot

Pole p1 introduces a 90 degree phase shift and gain reduces by 20db/decade. At the crossing point of 0dB the slope is 20dB/decade which is ok for the stability of the amplifier.

Now, lets assume that there is some parasitic capacitance in the feedback network which creates a bode plot seen in Plot 4. Pole p1 introduces a 90 degree phase shift in β and a 20dB/decade decrease rate.

Plot 4. Negative feedback with capacitance

Now, combining the open loop bode plot with the negative feedback plot we have the following plot (Plot 5).

Plot 5. Loop gain bode plot with capacitance in the negative feedback network

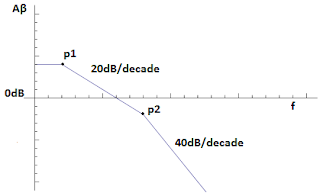
The capacitance which created a pole in the feedback network, introduced a second pole p2 in the loop gain bode plot. Pole p1 introduced 90 degree phase shift and ploe p2 another 90 degree phase shift. After p2 the slope is 40dB/decade. As p2 is above the 0dB crossing point, the slope is 40dB/decade at 0dB, meaning that enough phase shift is acquired to make the system probably unstable.

 In general we do not want the slope of the plot to be above 20db/decade at the crossing point (where gain is unity).

 Lets consider the use of an opamp in a non-inverting configuration as a voltage follower in Fig. 2.

Fig.2 Voltage follower

Being a voltage follower we know that the loop gain is equal to the open loop gain:
$$ A_{o}=A_{o} \cdot \beta $$
because β = 1.

The vast majority of the opamps in the market have an open loop gain bode plot as in Plot 1, where the slope is 20db/decade at the 0dB crossing point. Because β=1, the loop gain bode plot will be the same as the open loop gain bode plot and the amplifier is stable.
Nevertheless, there are some opamps out there which have an open loop bode plot like Plot 6.

Plot 6. Open loop gain bode plot of a market opamp

Because β = 1, the loop gain bode plot will be the same. We see that two poles (p1, p2) exist above the 0dB line, so the slope after p2 is 40dB/decade, resulting in an unstable amplifier.


So, what do we do to bring the amplifier in a stable situation?

One solution is to bring the pole p2 under the 0dB line, in order the slope to be 20dB/decade at the 0dB line. To do these we must add a voltage divider network in the feedack loop to reduce β, as seen in Fig. 3. In this case β = 1/10.
Of course the price to pay is that the closed loop gain of the amplifier is increased and is not more a true voltage follower.

Fig 3. Negative feedback with voltage devider

The result, will be a plot similar to Plot 6, but decreased in magnitude, so pole p2 is below 0dB and the slope at the 0dB crossing point is 20dB/decade (Plot 7).

Plot 7. Loop gain bode plot for stable amplifier

After p1 the slope is 20dB/decade, reaching pole p2 after which the slope is 40dB/decade, but does not concern us because the loop gain at that point is below 0dB (unity) and cannot result in oscillation.